Think of the wheather map: isobars depict the air pressure. The pressure is measured at discrete points, but for the wheather map, values in-between the measurement points are needed.
For the regression analysis -- as the model functions -- a product of Legendre polynomials is used. These are orthogonal functions on the interval [-1, 1]. So a robust regression can be computed in all cases (if the measurement points are well spread over the area in process). This technique requires a coordinate tranformation on the interval [-1, 1] and the fitting-function f(x1, x2) is not accurat outside the specified area.
To use this code, save this as 'XYRegression.bas' first.
Code: Select all
' This is file "XYRegression.bas"
' (C) LGPLv2 by Thomas[ dot ]Freiherr{ at }gmx{ dot }net
#INCLUDE ONCE "fbmath.bi"
#INCLUDE ONCE "LegendrePolynom.bas"
#DEFINE XYR_INDEX(_L_,_H_) _L_ += 1 : IF _L_ >= Basis THEN _L_ = 0 : _H_ += 1
TYPE XYRegression
AS STRING Err_
DECLARE CONSTRUCTOR(V() AS DOUBLE, BYVAL O AS UINTEGER)
DECLARE CONSTRUCTOR(V() AS DOUBLE, BYVAL O AS UINTEGER, _
BYVAL Xn AS DOUBLE, BYVAL Xx AS DOUBLE, _
BYVAL Yn AS DOUBLE, BYVAL Yx AS DOUBLE)
DECLARE DESTRUCTOR()
DECLARE FUNCTION Val_(BYVAL X AS DOUBLE, BYVAL Y AS DOUBLE) AS DOUBLE
DECLARE FUNCTION Abw_(V() AS DOUBLE) AS DOUBLE
Private:
AS LegendrePolynom PTR Leg ' polynoms to use
AS STRING ResStr ' memory to store results
AS DOUBLE PTR Res ' pointer to use memory
AS DOUBLE Xmin, Ymin, Dx, Dy ' for transformation interval [-1, 1]
AS INTEGER Basis, Lines ' for indexing
DECLARE SUB Fit_(V() AS DOUBLE)
END TYPE
CONSTRUCTOR XYRegression(V() AS DOUBLE, BYVAL O AS UINTEGER)
Basis = O + 1
VAR kx = LBOUND(V, 2), ky = kx + 1, od1 = LBOUND(V, 1)
IF UBOUND(V, 2) = kx + 2 THEN
Xmin = V(od1, kx) : Ymin = V(od1, ky)
VAR Xmax = Xmin, Ymax = Ymin
FOR i AS INTEGER = od1 TO UBOUND(V) ' search extrema
IF V(i, kx) < Xmin THEN Xmin = V(i, kx)
IF V(i, kx) > Xmax THEN Xmax = V(i, kx)
IF V(i, ky) < Ymin THEN Ymin = V(i, ky)
IF V(i, ky) > Ymax THEN Ymax = V(i, ky)
NEXT
Dx = Xmax - Xmin : IF Dx THEN Dx = 2 / Dx
Dy = Ymax - Ymin : IF Dy THEN Dy = 2 / Dy
END IF
Fit_(V())
END CONSTRUCTOR
CONSTRUCTOR XYRegression(V() AS DOUBLE, BYVAL O AS UINTEGER, _
BYVAL Xn AS DOUBLE, BYVAL Xx AS DOUBLE, _
BYVAL Yn AS DOUBLE, BYVAL Yx AS DOUBLE)
Basis = O + 1
Xmin = Xn : Ymin = Yn ' compute extrema
Dx = Xx - Xn : IF Dx THEN Dx = 2 / Dx
Dy = Yx - Yn : IF Dy THEN Dy = 2 / Dy
Fit_(V())
END CONSTRUCTOR
DESTRUCTOR XYRegression()
IF Leg THEN DELETE Leg
END DESTRUCTOR
FUNCTION XYRegression.Val_(BYVAL X AS DOUBLE, BYVAL Y AS DOUBLE) AS DOUBLE
VAR xx = (X - Xmin) * Dx, yy = (Y - Ymin) * Dy
VAR r = 0.0, n = 0, m = 0
FOR i AS INTEGER = 0 TO Lines
r += Res[i] * Leg->Val_(xx, n) * Leg->Val_(yy, m)
XYR_INDEX(n, m)
NEXT : RETURN r
END FUNCTION
FUNCTION XYRegression.Abw_(V() AS DOUBLE) AS DOUBLE
VAR i = 0, kx = LBOUND(V, 2), ky = kx + 1, kz = kx + 2, d = 0.0
FOR i = LBOUND(V, 1) TO UBOUND(V, 1)
d += (V(i, kz) - Val_(V(i, kx), V(i, ky))) ^ 2
NEXT : RETURN d / (i - LBOUND(V, 1))
END FUNCTION
SUB XYRegression.Fit_(V() AS DOUBLE)
VAR od2 = LBOUND(V, 2)
IF UBOUND(V, 2) - od2 <> 2 THEN Err_ = "field dimension" : EXIT SUB
IF Dx = 0 THEN Err_ = "no X difference" : EXIT SUB
IF Dy = 0 THEN Err_ = "no Y difference" : EXIT SUB
VAR od1 = LBOUND(V, 1), az = UBOUND(V, 1) - od1
Lines = Basis ^ 2 - 1
IF az < Lines THEN Err_ = "less values" : EXIT SUB
Leg = NEW LegendrePolynom(Basis - 1)
DIM AS DOUBLE w(Lines, Lines + 1), x(az), y(az)
Xmin += 1 / Dx : Ymin += 1 / Dy
VAR kx = od2, ky = kx + 1, kz = kx + 2, p = od1
FOR i AS INTEGER = 0 TO az ' transform into [-1, 1]
x(i) = (V(p, kx) - Xmin) * Dx
y(i) = (V(p, ky) - Ymin) * Dy
p += 1
NEXT
VAR m = 0, n = 0
FOR i AS INTEGER = 0 TO Lines ' build linear equation system
VAR j = 0, k = 0, p = 0, q = 0
FOR k = 0 TO Lines ' left side
VAR sum = 0.0
FOR j = 0 TO az
sum += Leg->Val_(x(j), n) * Leg->Val_(y(j), m) * _
Leg->Val_(x(j), p) * Leg->Val_(y(j), q)
NEXT : w(i, k) = sum / j
XYR_INDEX(p, q)
NEXT
VAR sum = 0.0
FOR j = 0 TO az ' right side
sum += Leg->Val_(x(j), n) * Leg->Val_(y(j), m) * V(j + od1, kz)
NEXT : w(i, k) = sum / j
XYR_INDEX(n, m)
NEXT
VAR det = .0 ' solve system
GaussJordan(w(), det)
IF ErrCode THEN Err_ = "system unsolvable (fbmath code = " & ErrCode & ")" : EXIT SUB
VAR k = Lines + 1
ResStr = STRING(8 * k, 0) ' save results
Res = CAST(DOUBLE PTR, SADD(ResStr))
FOR i AS INTEGER = 0 TO Lines
Res[i] = w(i, k)
NEXT
END SUBHandling
- You'll need two add-ons: fbmath.bi and LegendrePolynom.bas.
Use VAR test = XYRegression(V(), Order, x1Min, x1Max, x2Min, x2Max) in order to create a new fitting-function named as test, which is best-matching the measurement values in V():
. The parameter V() contains an array of DOUBLE values, 3 coloumns x1, x2, y (dimension# 2). The lines (dimension# 1) contains the measurement trippels. (Be careful, each line will be evaluated -- even unset values.)
. The parameter Order declares the order of the Legendre polynomials. So it's to specify the maximum number of extrema in the specified area. An order of 4 means that (4 - 1) ^ 2 = 9 extrema can be at the map. The higher the order, the more accurat the fitting-function may be. But a high order needs more execution time and means higher memory consumption (= 8 * (order + 1) ^ 2 after dim operation).
. The parameters x1Min, x1Max and x2Min, x2Max declares the accurat area. The fitting-function should not be used outside this area. You may declare this area or omit the parameters. In the last case the borders are set as the extremas of the input values in V().
Use the function test.Abw_(V()) to compute the least squares. Low values determine good curve fitting.
Use test.Val_(x1, x2) to compute the fitting-function.
Code: Select all
' This is file "XYRegressionTest.bas"
' (C) GPLv3 by Thomas[ dot ]Freiherr{ at }gmx{ dot }net
#INCLUDE "XYRegression.bas"
' function to generate some test values
FUNCTION fn(BYVAL Xx AS DOUBLE, BYVAL Yy AS DOUBLE) AS DOUBLE
VAR x = (xx - 379) / 319, y = (yy - 112) / 199
RETURN 3 * EXP(-(x * x + y * y)) * SIN(x * y + 3)
END FUNCTION
' prepare graphics
CONST ScW = 639, ScH = 399
SCREENRES ScW + 1, ScH + 1
WINDOWTITLE "Only grey colors are valid, others are inaccurat areas."
' Prepare some test values, V() has 3 coloumns: x1, x2, y
CONST Anzahl = 69 ' play with this number to see the differences
CONST chx1 = 0, chx2 = chx1 + 1, chy = chx1 + 2
DIM AS DOUBLE V(Anzahl, chy)
FOR i AS INTEGER = 0 TO Anzahl
VAR xx = RND * ScW
VAR yy = RND * ScH
V(i, chx1) = xx
V(i, chx2) = yy
V(i, chy) = fn(xx, yy)
NEXT
' Compute regression analysis
CONST Order = 4 ' play with this number to see the differences
VAR test = XYRegression(V(), Order, 0, ScW, 0, ScH)
IF LEN(test.Err_) THEN ' on error
?"Fehler: "; test.Err_
ELSE' regression analysis OK
VAR mx = V(0, chy), mn = mx' check extrema (for coloring)
FOR i AS INTEGER = 1 TO Anzahl
IF V(i, chy) > mx THEN mx = V(i, chy)
IF V(i, chy) < mn THEN mn = V(i, chy)
NEXT
VAR f = mx - mn : IF f THEN f = 15 / f ' draw colored area
FOR x AS INTEGER = 0 TO ScW
FOR y AS INTEGER = 0 TO ScH
VAR col = 16 + CUINT((test.Val_(x, y) - mn) * f)
PSET (x, y), col
NEXT
NEXT
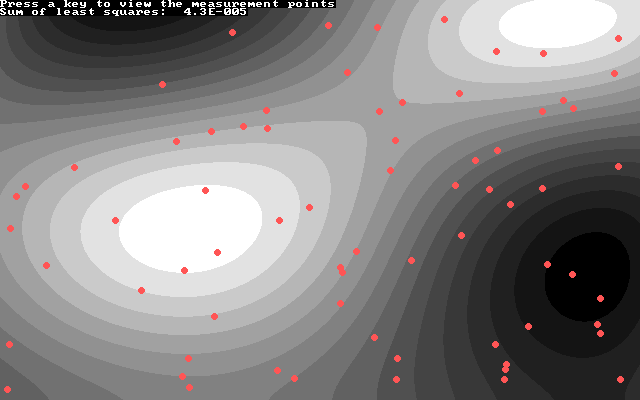
PRINT "Press a key to view the measurement points"
SLEEP
FOR i AS INTEGER = 0 TO Anzahl ' draw measurement points
CIRCLE (V(i, chx1), V(i, chx2)), 3, 12, , , ,F
NEXT
PRINT USING "Sum of least squares: ##.#^^^^^"; test.Abw_(V())
END IF
SLEEP- Check this link for possible updates.
http://www.freebasic-portal.de/code-bei ... e-210.html
